마르코프 체인에 관하여
신기훈 | 4월 23일, 2019 | 8분 읽기
일상생활에서 우리는 정해진 순서대로 생활하기도 하지만 중요한 상황에서 어떤 선택을 해야 할지 고민하는 경우 역시 많습니다. 예를 들면 ‘점심시간에 한식을 먹을지, 중식을 먹을지’와 같은 사소한 선택이 있는가 하면 ‘이사할 집을 어디로 할지’와 같은 심각한 선택을 해야 하는 순간이 올 때도 많습니다.
이런 상황에서 사람들은 ‘현재 몇 가지의 선택지가 있고, 과거 비율을 충분한 횟수로 명할 수 있다면 미래에 특정한 선택지를 고를 확률에 대해서도 표현할 수 있지 않을까’라는 고민을 하게 됩니다.
기업의 경우 예를 들어 쇼핑몰에서는 특정 조건의 고객군이 로그인 후 어떤 검색을 거쳐 장바구니에 넣고 최종 결재를 하게 되었는지, 그리고 해당 조건의 고객군이 미래에 어떠한 선택을 하게 될 것인지 궁금해할 것입니다.
이때 접근해볼 수 있는 방법 중 하나인 마르코프 체인(Markov chain)를 간략히 소개하겠습니다.
마르코프 체인(Markov chain)이란?
마르코프 체인의 정의란 마르코프 성질을 가진 이산 확률과정을 뜻합니다. 여기서 마르코프 성질은 ‘특정 상태의 확률은 오직 과거의 상태에 의존한다’라는 것입니다. 예를 들어 오늘의 날씨가 맑다면 내일의 날씨는 맑을지 비가 내릴지를 확률적으로 표현할 수 있습니다. 물론 실제 날씨 예보라는 건 굉장히 복잡한 변수들과 모델링을 거쳐서 생성되지만 이러한 연속적인 현상을 단순히 표현할 때는 마르코프 체인을 가정하고 쓸 수 있고, 종종 단순한 모델이 강력한 효과를 발휘할 때도 있습니다.
이제 마르코프 체인을 통해 오늘 날씨를 통해 내일의 날씨를 확률적으로 예측하고, 다시 내일의 날씨 정보에 기반해서 모레의 날씨를 예측하는 행위를 충분히 반복했다고 가정하겠습니다. 그리하여 내일 날씨에 관한 확률의 묶음이 특정 성질을 반복할 때 반복 계산의 어느 지점에서 날씨가 흐릴지, 비가 올지, 맑을지에 대한 확률이 특정하게 수렴하게 될 것입니다. 따라서 마르코프 체인은 오늘 흐림이라서 내일은 무조건 비가 아니라 내일도 흐릴 확률은 어느 정도인지, 혹은 맑거나 눈이 내릴 확률은 어느 정도인지 확률적으로 표현하게 됩니다. 그래서 마코프 체인에서는 상태 전이 확률이 핵심이 되고 아래와 같은 상태 전이도로 표현할 수 있게 됩니다.
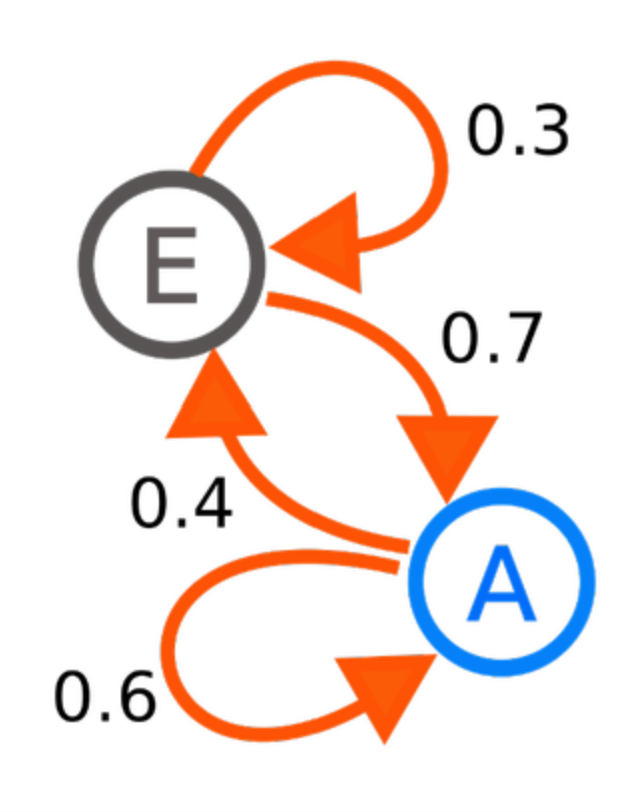
[Wipedia] 마르코프 체인 예시
도표에서는 상태 A에서 상태 E로 전이할 확률을 0.4 반대의 확률을 0.7이고 상태 E와 A를 반복할 경우에는 각각 0.3과 0.6으로 보았습니다. 이제 간단한 예제를 통하여 마르코프 체인 계산 방법에 대해 알아보겠습니다.
마르코프 체인 계산 방법
예제는 앞서 언급한 날씨를 예로 들겠습니다. 실제로는 날씨도 맑음, 흐림, 비, 눈, 태풍 등 매우 다양한 조건이 있지만 여기서는 최대한 간단히 설명하기 위해 맑음, 흐림 2가지의 조건만 설명하도록 하겠습니다.
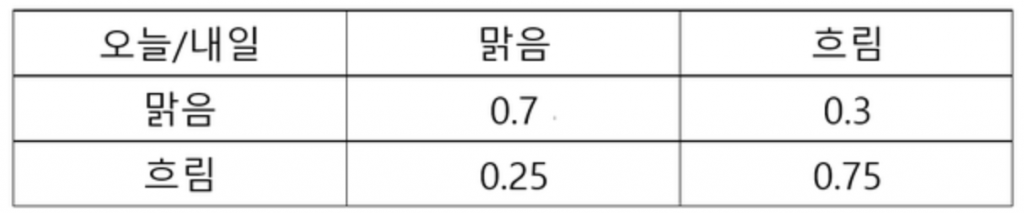
위와 같은 확률이 있을 때 우리는 아래와 같이 상태 전이도를 그릴 수 있습니다. 위의 표와 동일하게 맑음이 내일도 계속될 확률은 0.7, 맑음에서 흐림으로 갈 확률은 0.3 등으로 표현할 수 있습니다.
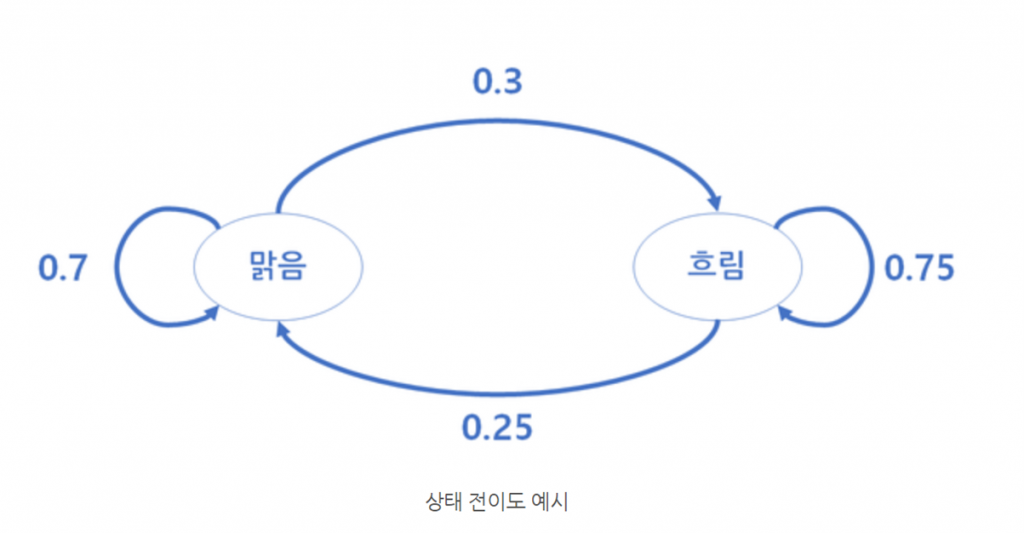
이를 아래와 같은 전이확률 행렬로 표현할 수 있습니다.
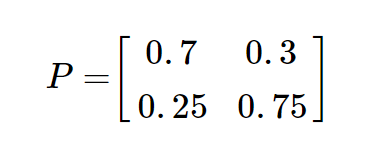
전이행렬을 가지고 모레는 날씨가 어떨지 확률 변화를 계산해보겠습니다.
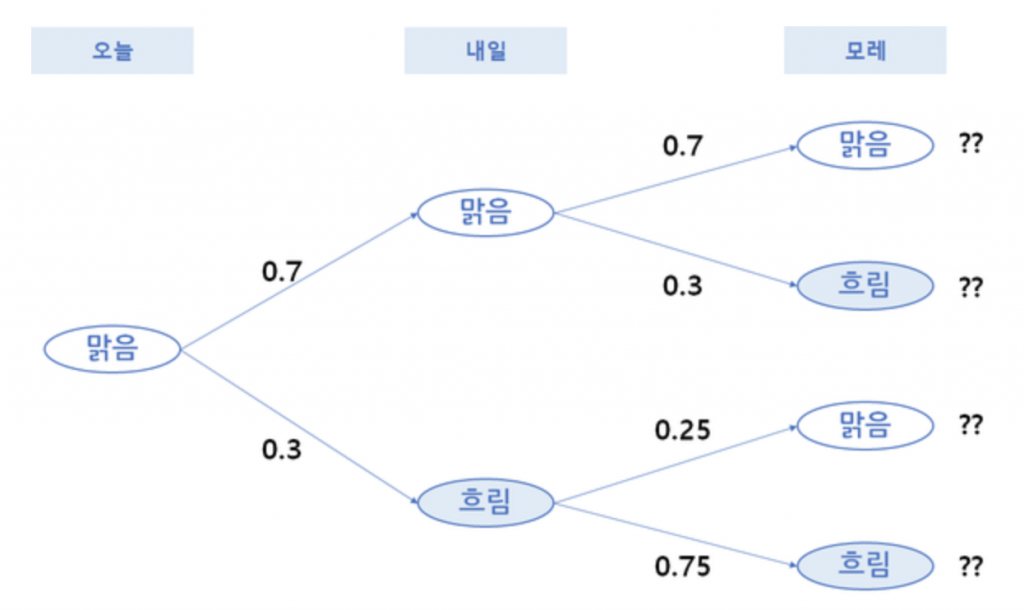
위의 전이 흐름도를 가지고 계산을 했을 때 행렬곱을 통하여 아래와 같이 계산할 수 있습니다. 다시 말해 모레의 확률 변화는 오늘과 내일의 전이가 연속되어 일어나는 경우이기 때문에 전이행렬을 곱하여 계산하게 됩니다.
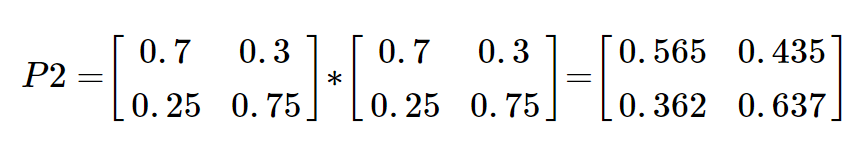
만약 지난 3년간 특정 일의 날씨 중 80%가 맑았다면 특정일 기준 모레가 맑음 확률은 0.8 x 0.565 + 0.2 x 0.362 = 0.524이기 때문에 52.4% 확률로 예측할 수 있게 됩니다.
이러한 상태에서 충분히 많은 횟수를 반복한다면 어느 순간에는 전이행렬이 변하지 않는 상태가 오는데 이를 두고 안정상태(steady state)라 부르고, 확률이 직전 상태와 동일하게 수렴하게 됩니다. 이러한 확률 분포를 정적분포(Stationary Distribution)라고 부르게 됩니다.
마르코프 체인 사용 예시 – 구글 페이지 랭크 알고리즘
마르코프 연쇄 활용으로 가장 많이 알려진 것은 구글 페이지 랭크 알고리즘입니다. 타 블로그에서 소개한 내용을 각색해서 간단히 예를 들면 개인 홈페이지가 4개가 있고 네이버 홈페이지 1개 이렇게 총 5개의 홈페이지가 있고, 인터넷으로 상호 연결되어 있는 상태를 가정해보겠습니다. 각 홈페이지마다 주인들이 달아 놓은 임의의 링크들이 있을 테고 그 링크를 타고 bot이 돌아다닌다고 가정했을 때 특정 시점에 bot을 정지시키면 bot이 위치하고 있을 확률이 가장 높은 곳은 어디일까요?
대부분의 사람들은 당연히 네이버를 선택할 것입니다. 왜냐하면 링크라는 것은 보다 많은 정보를 확인하기 위한 연결인데 개인 홈페이지보다 네이버에 보다 많은 자료들이 존재할 것이라고 생각하기 때문입니다. 이러한 가정을 가지고 구글 페이지 랭크 알고리즘은 특정 순간에 각 페이지에 머물 확률을 가지고 추가적인 알고리즘 및 튜닝을 더 하여 각 페이지의 랭킹 및 점수를 선정하게 됩니다.
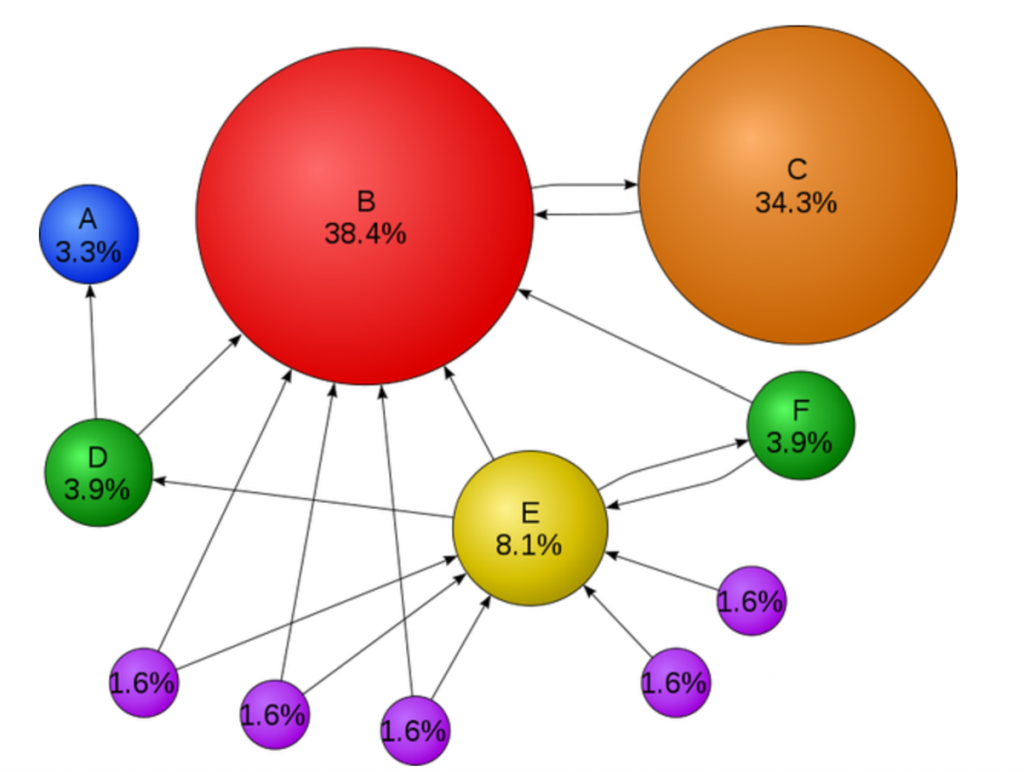
[Wipedia] 구글의 선택을 받으려면 많은 화살표를 받자
프로세스 마이닝에는 어떻게?
프로세스 분석 관점에서 마르코프 체인을 활용하여 당장 할 수 있는 일은 특정 프로세스 패턴이 발생할 확률을 알아낼 수 있는 것입니다. 그리고 이를 응용하여 특정 패턴 형태의 프로세스가 일정 부분 진행된 상태일 때 잔여 프로세스가 특정 패턴으로 진행할 확률 및 프로세스 완료까지의 잔여 시간을 예측할 수 있을 것입니다.
이외에 마르코프 체인에서 좀 더 나아가서 은닉 마르코프 모델(hidden Markov model)을 활용하여 결과 패턴만 있을 경우 숨겨진 프로세스 패턴을 탐색하기도 합니다. 은닉 마르코프 모델 등은 다음 시간에 다뤄보도록 하겠습니다.
References
https://ratsgo.github.io/machine%20learning/2017/03/18/HMMs/
https://operatingsystems.tistory.com/entry/Data-Mining-Markov-Chain-and-Hidden-Markov-Model

