Markov Chains: Definition and Examples
Kihoon Shin | Apr 23, 2019 | 8 min read
In our daily lives, we often find ourselves making decisions in a certain order, but there are also moments of significance where we need to ponder our choices. For instance, we might contemplate whether to have Korean or Chinese cuisine for lunch, or we might face a more serious decision like choosing a new place to live.
In such situations, people might wonder, “If we have a few options at hand and we can observe the past patterns with sufficient frequency, could we also predict the probability of making a certain choice in the future?”
For businesses, consider an online store where specific groups of customers, under certain conditions, log in, search for items, add them to their cart, and proceed to checkout. The business might be interested in knowing what kind of choices these customer groups will make in the future.
In this context, one approach to consider is the Markov chain, which I will briefly introduce here.
What is Markov chain?
A Markov chain refers to a discrete probabilistic process with the Markov property. The Markov property states that the probability of a particular state depends solely on the previous states. For example, if today’s weather is clear, we can probabilistically express whether tomorrow’s weather will be clear or rainy. Of course, actual weather forecasts involve complex variables and modeling, but for the sake of simple representation of such continuous phenomena, we assume and utilize Markov chains. Sometimes, even a simple model can have a powerful impact.

what is the probability of snow tomorrow?
Now, let’s use the Markov chain to probabilistically predict tomorrow’s weather based on today’s weather, and then repeat this process to predict the weather for the day after tomorrow using tomorrow’s weather information. Let’s assume that we have repeated this process sufficiently. As a result, bundles of probabilities about tomorrow’s weather will converge in a way that certain properties repeat themselves in the sequence of calculations. Consequently, the Markov chain allows us to probabilistically express the likelihood that if it’s cloudy today, it won’t necessarily rain tomorrow but the probability of it being cloudy tomorrow, or the likelihood of it being clear or snowy tomorrow. In the Markov chain, the transition probabilities between states play a crucial role, and these transitions can be represented using transition diagrams like the one below.
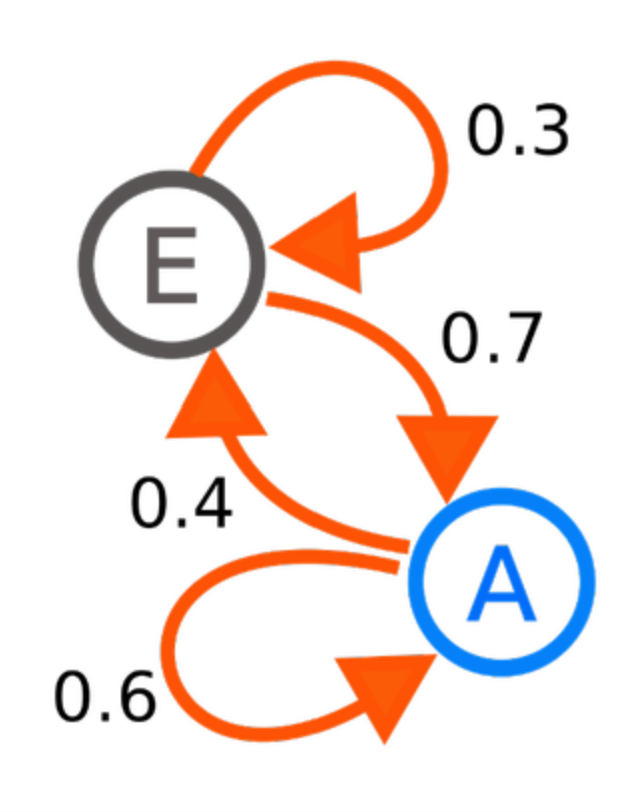
[Wikipedia] Example of Markov Chain
In the diagram, the transition probability from state A to state E is 0.4, and the reverse probability is 0.7. When transitioning between states E and A repeatedly, the probabilities are 0.3 and 0.6, respectively. Now, let’s explore the calculation method of the Markov chain through a simple example.
Calculation Method of Markov Chain
For this example, let’s use the weather as mentioned earlier. In reality, weather conditions include a wide variety such as sunny, cloudy, rainy, snowy, and stormy. However, for the sake of simplicity in explanation, we will consider only two conditions: sunny and cloudy.

Given such probabilities, we can draw a state transition diagram as shown below. Similar to the table above, we can represent that the probability of “Clear” weather continuing tomorrow is 0.7, and the probability of transitioning from “Clear” to “Cloudy” is 0.3, and so on.
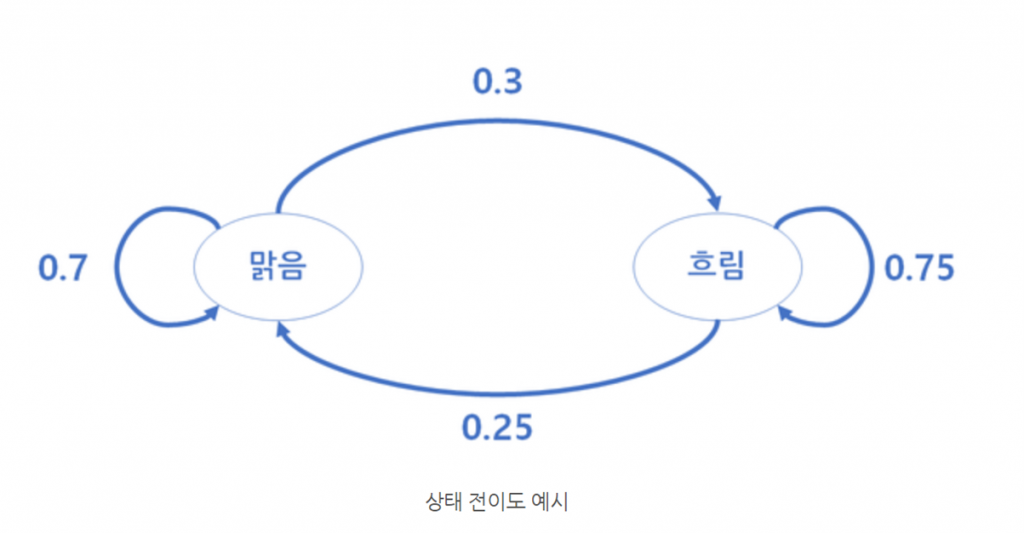
State Transition Diagram Example
This can be represented by the following transition matrix.
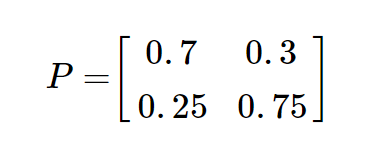
State-transition Matrix
This can be represented by the following transition probability matrix:
Using the transition matrix, let’s calculate how the probability of weather conditions might change for the day after tomorrow.
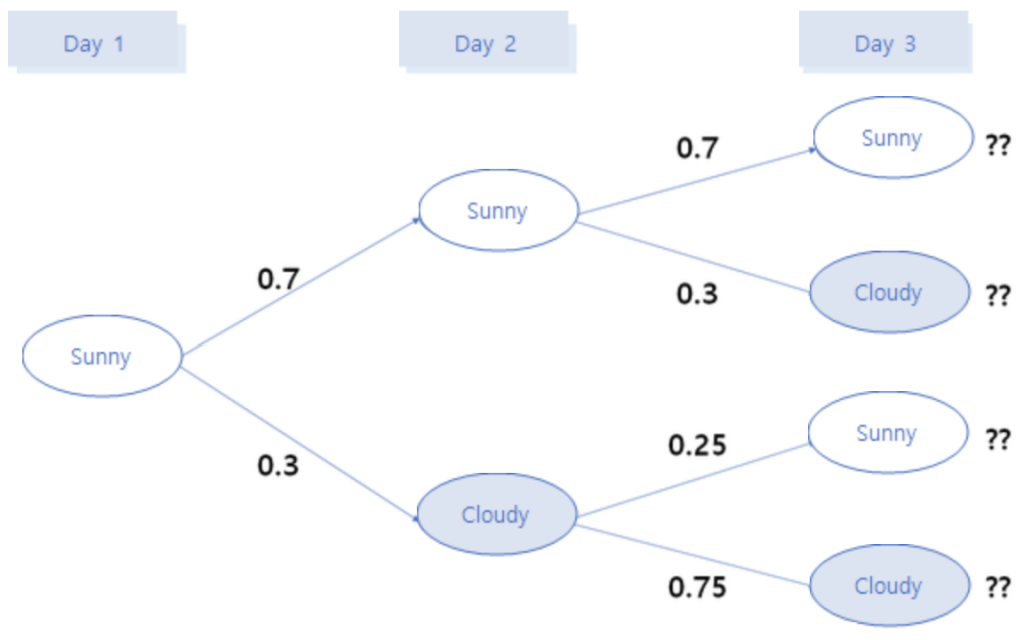
When we know today’s and tomorrow’s weather, what percentage of the day after tomorrow’s weather will be sunny or cloudy? Using the given transition diagram, we can calculate this through matrix multiplication as follows. In other words, the probability change for the day after tomorrow is the result of continuous transitions from today to tomorrow and then to the day after tomorrow, which is why we multiply the transition matrices to calculate it.
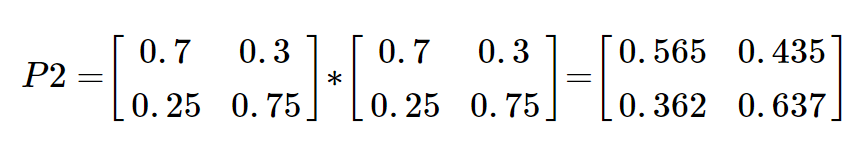
If, over the past 3 years, 80% of specific days had clear weather, then based on a specific day, the probability of having clear weather the day after tomorrow would be calculated as 0.8 x 0.565 + 0.2 x 0.362 = 0.524, resulting in a prediction with a probability of 52.4%.
In this scenario, if you repeat the process a sufficient number of times, there will come a point where the transition matrix doesn’t change anymore. This is referred to as the steady state, and the probabilities will converge to be the same as the previous state. This probability distribution is called the stationary distribution.
Markov Chain Use Case: Google Page Rank Algorithm
One of the most well-known applications of the Markov chain is the Google PageRank algorithm. Let’s adapt the explanation from another blog and provide a simple example. Suppose there are a total of 5 websites: 4 personal websites and 1 Google, all interconnected on the internet. Each website has randomly placed links, and we assume that a bot navigates through these links. If we stop the bot at a specific point, where is the most likely place for the bot to be?
Most people would naturally choose Google. Why? Because links are connections to access more information, and it’s expected that Google would have more information than individual websites. With this assumption, the Google PageRank algorithm calculates the probability of the bot being on each page at a given time. By incorporating additional algorithms and tuning, the PageRank algorithm determines the ranking and scores for each page.
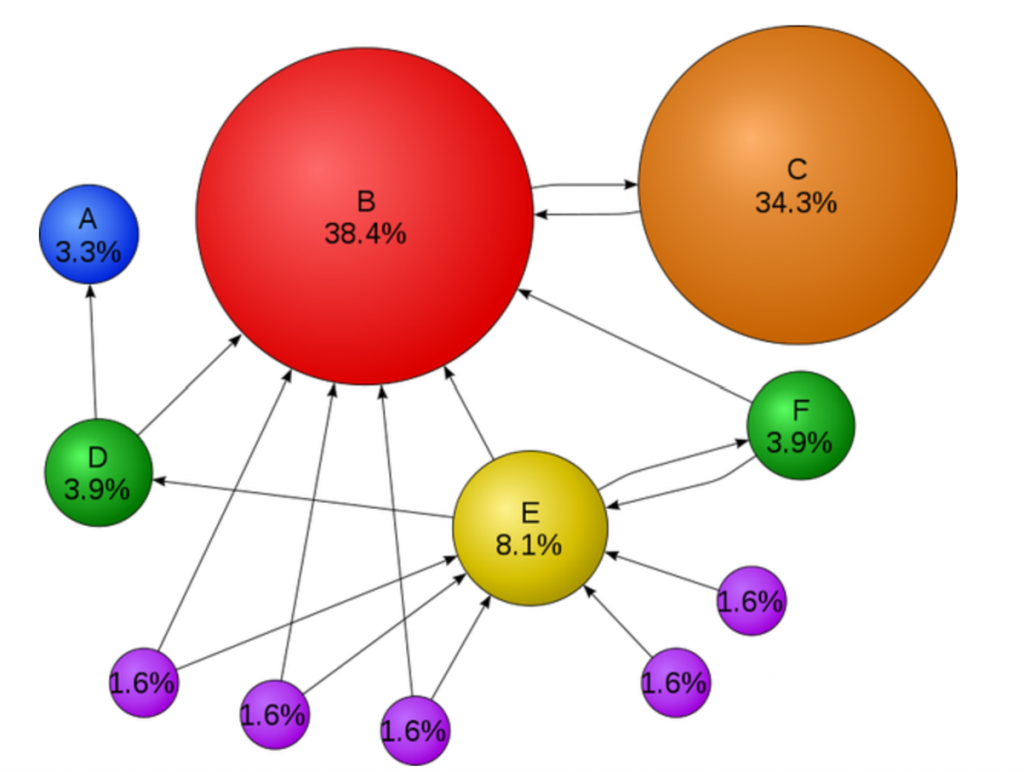
[Wikipedia] In order to get chosen by Google, receive many arrows
How does process mining work with Markov Chain?
From a process analysis perspective, using Markov Chains in Process Mining allows us to immediately determine the probability of specific process patterns occurring. Furthermore, this can be extended to predict the probability of residual processes continuing with a certain pattern when a specific pattern-shaped process has progressed to a certain point. Additionally, it becomes possible to predict the remaining time until process completion.
References
https://ratsgo.github.io/machine%20learning/2017/03/18/HMMs/
https://operatingsystems.tistory.com/entry/Data-Mining-Markov-Chain-and-Hidden-Markov-Model